Linear Time Invariant System Properties

Additivity A system islineari Ta 1 x 1n a 2 x 2n a 1 Tx 1n a 2 Tx 2n I Additivity. Systems that are not time-invariant are called time-varying. Linear time-invariant systems LTI systems are a class of systems used in signals and systems that are both linear and time-invariant. For system E a simple substitution of the summation index shows you that the system is indeed time-invariant. In system analysis among other fields of study a linear time-invariant system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance. So here we will consider LTI system properties in detail. Underthe conditionof initial restthe system is linear time -invariant LTI andcausal Theconditionof initial rest does not specifya zero initial conditionat afixed point oftimebut rather adjusts this pointin time so that theresponseis zero untilthe inputbecomes nonzero For example ifxt0for t.

Linear Time Invariant Systems.

In system analysis among other fields of study a linear time-invariant system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance. Properties of Linear Time Invariant Systems. This is not the case for a linear time-varying system. H k n h 0 n k. Any delay provided in the input must be reflected in the output for a time invariant system. In particular a necessary and sufficient condition for causality in the case of linear time-invariant systems is that the impulse response be 0 for t less than 0 in the continuous-time case or for n less than 0 in the discrete-time case.

Properties Of Linear Time Invariant Systems And Various Transforms Mcgraw Hill Education Access Engineering

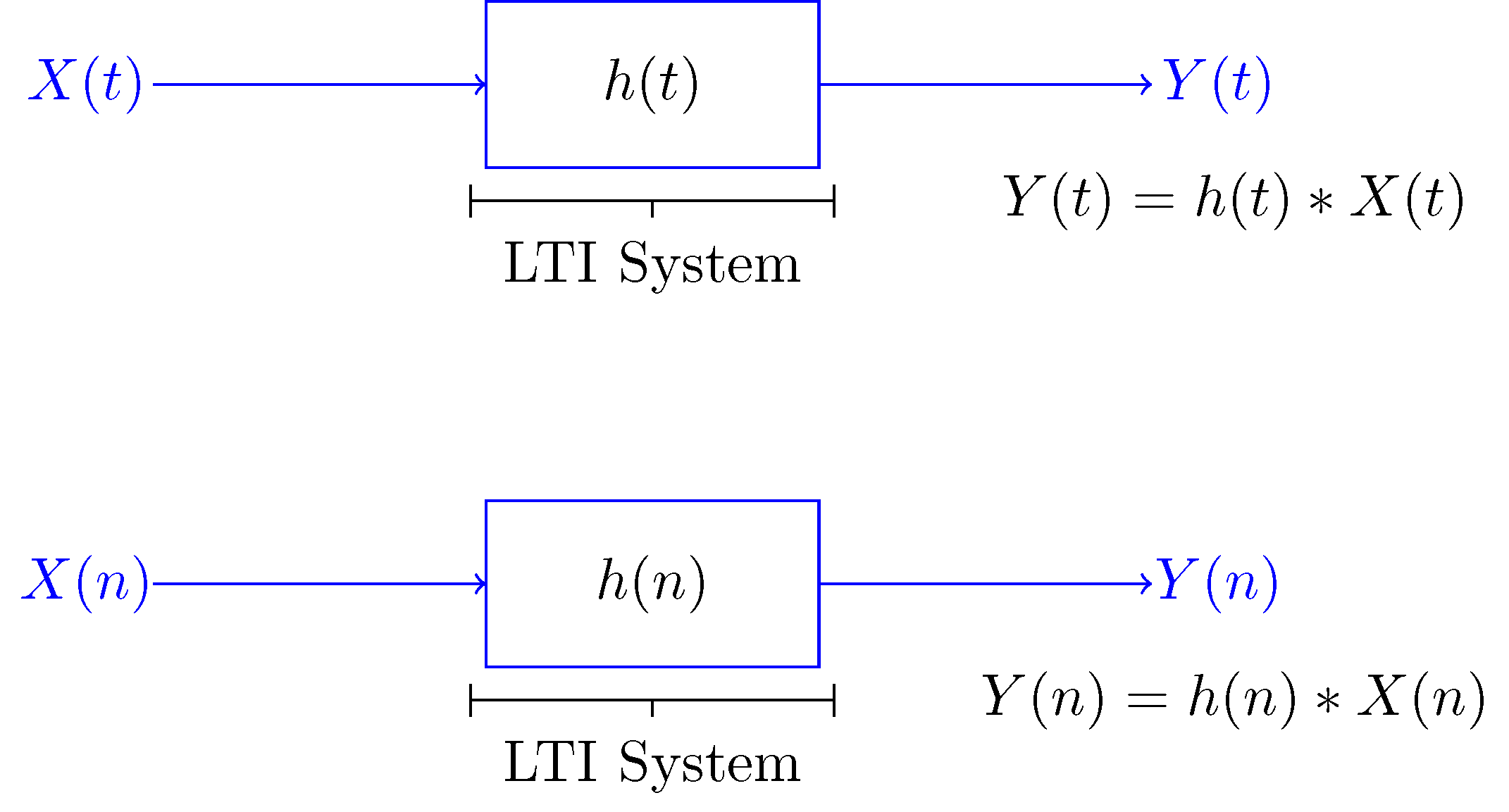
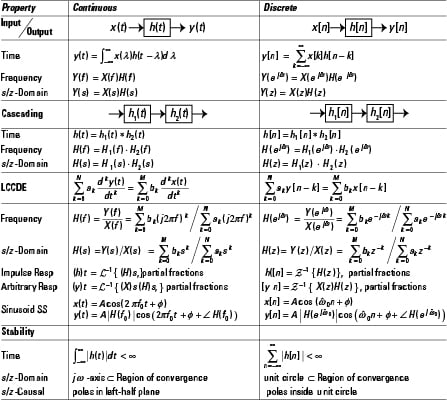
Linear time invariant system properties. The three basic properties of convolution as an. Just answer the question does the output signal at any time depend on future values of the input signal If the answer is no then the system is causal otherwise it isnt. In discrete time displaystyle xn ast hn hn ast xn displaystyle Sigma_-inftyinfty hk xn-k In continuous time displaystyle xt ast ht ht ast xt displaystyle int_-inftyinfty htau xt tau dtau.

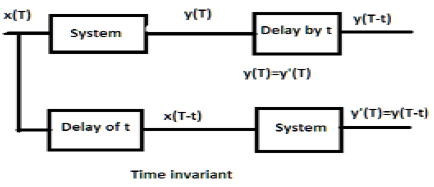
Time invariance is the property of a system which makes the behavior of the system independent of time. If the linear system is time invariant then the responses to time-shifted unit impulses are all time-shifted versions of the same impulse responses. Supplementary Notes for ELEN 4810 Lecture 2 Introduction to Linear Time Invariant Systems John Wright Columbia University September 20 2021 Disclaimer.

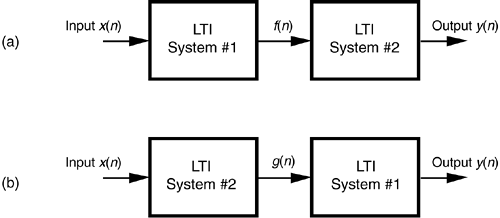
Tx 1n x 2n Tx 1n Tx 2n x 1nT y 1n x 2nT y 2n x 1n x 2nT y 1n y 2n for any input sequences x 1n and x 2n. One has to specify all the. This is not the case for a linear time-varying system.

We can always writexn P rxrδnr HenceH xnH P rxrδn r LTI Systems. So for linear time-invariant systems causality is equivalent to the impulse response being 0 up until t or n equal to 0. Let a 1 a 2 1.

This post covers properties of LTI system. In particular a necessary and sufficient condition for causality in the case of linear time-invariant systems is that the impulse response be 0 for t less than 0 in the continuous-time case or for n less than 0 in the discrete-time case. For system E a simple substitution of the summation index shows you that the system is indeed time-invariant.

Time InvariantynH xn ynrH xnrr. Introduction to LTI systems2. 24 Therefore the impulse responsehn h 0 n of an LTI system characterizes the system completely.

Linear time-invariant systems LTI systems are a class of systems used in signals and systems that are both linear and time-invariant. Linear systems are systems whose outputs for a linear combination of inputs are the same as a linear combination of individual responses to those inputs.

Properties Of Lti Systems Ppt Download

2 3 Properties Of Linear Time Invariant Systems Ppt Download

A A Linear Time Invariant Lti System Takes An Input Signal And Download Scientific Diagram

Lti System Properties Example

Linear Time Invariant Lti Systems Youtube

Ece205 Lecture 4 1 System Properties Linearity And Time Invariance Youtube

Properties Of Linear Time Invariant Systems And Various Transforms Mcgraw Hill Education Access Engineering

Solved 2 A Property Of Linear Time Invariant Systems Is Chegg Com

Properties Of Lti Systems Ppt Download

Properties Of Lti Systems Discussion With Solved Examples 2 3 Youtube

Chapter 10 Discretetime Linear Timeinvariant Systems Sections 10

Linear Time Invariant Lti Systems With Random Inputs

A A Linear Time Invariant Lti System Takes An Input Signal And Download Scientific Diagram

Solved 2 Linear Time Invariant Property Suppose That S Is Chegg Com

Introduction To Linear Time Invariant System Descriptions Youtube

Linear Time Invariant System Wikipedia

Ppt Linear Time Invariant Systems Powerpoint Presentation Free Download Id 5500957

Linear Time Invariant Lti System Step Response Electricalworkbook

Linear Time Invariant System What Is A Lti System Lti System Superposition And Time Invariance Youtube

Solved A Discrete Time Linear Time Invariant System H Is Chegg Com

Linear Time Invariant System Wikipedia

Time Domain Representation Of Linear Time Invariant Lti Ppt Video Online Download

Properties Of Linear Time Invariant Systems And Various Transforms Mcgraw Hill Education Access Engineering

Linear Time Invariant System

System Properties Linear Causal Time Invariant Stable Signal Processing Stack Exchange

The Commutative Property Of Linear Time Invariant Systems Chapter One Discrete Sequences And Systems

Properties Of Lti System

Lti System Properties Youtube

Dsp Time Invariant Systems

Recognizing System Properties And Classifications Dummies

Lecture 3 Signals Systems Concepts

Signal And Systems Prof H Sameti Chapter 2 1 Representation Of Dt Signals In Terms Of Shifted Unit Samples System Properties And Examples 2 Convolution Ppt Download

A Linear Time Invariant Discrete Time System Is Chegg Com

Time Variant Time Invariant Systems Signals Systems Engineerstutor

Doc Questions On Digital Signal Processing Priyanka Gupta Academia Edu

Fac Ksu Edu Sa

Properties Of Lti System

Linear Time Invariant And Causal Systems Youtube

Linear Time Invariant Systems And Their Frequency Response

2 0 Linear Timeinvariant Systems 2 1 Discretetime

Properties Of Linear Time Invariant Systems Impulse Respons

Solved Problem 5 10 Pts A Linear Time Invariant System Chegg Com

Shifted Input An Overview Sciencedirect Topics

2 2 Linear Time Invariant Systems Engineering Libretexts

Illustration Of A Linear Time Invariant Lti System Upper Row Time Download Scientific Diagram

Linear Time Invariant Systems Brilliant Math Science Wiki

Signals Systems Cnet 221 Chapter 3 Linear Time Invariant System Ppt Download

Linear Time Invariant System Wikipedia

1

In discrete time displaystyle xn ast hn hn ast xn displaystyle Sigma_-inftyinfty hk xn-k In continuous time displaystyle xt ast ht ht ast xt displaystyle int_-inftyinfty htau xt tau dtau.

These properties apply to many important physical systems in which case the response y of the system to an arbitrary input x can be found directly using convolution. This is not the case for a linear time-varying system. The three basic properties of convolution as an. H k n h 0 n k. If the linear system is time invariant then the responses to time-shifted unit impulses are all time-shifted versions of the same impulse responses. Tx 1n x 2n Tx 1n Tx 2n x 1nT y 1n x 2nT y 2n x 1n x 2nT y 1n y 2n for any input sequences x 1n and x 2n. For instance in a model of. We can always writexn P rxrδnr HenceH xnH P rxrδn r LTI Systems. These terms are briefly defined below.

Supplementary Notes for ELEN 4810 Lecture 2 Introduction to Linear Time Invariant Systems John Wright Columbia University September 20 2021 Disclaimer. This post covers properties of LTI system. For system E a simple substitution of the summation index shows you that the system is indeed time-invariant. Linear-time invariant systems that were partially discussed before play an important role in describing signals. Generally speaking any process can be described with the idea of Linear-Time Invariant systems. If the linear system is time invariant then the responses to time-shifted unit impulses are all time-shifted versions of the same impulse responses. Just answer the question does the output signal at any time depend on future values of the input signal If the answer is no then the system is causal otherwise it isnt.